Trapezoid Area Formula - Your Friendly Guide
Figuring out the amount of flat space inside a shape, especially one like a trapezoid, might seem a little tricky at first glance. It's actually a pretty straightforward process once you get the hang of it, and it all comes down to a neat little equation. This particular shape, with its two flat sides that run alongside each other, shows up more often than you might think in the things we see every day, from the way a roof is shaped to certain parts of a bridge. So, knowing how to measure its inner expanse can be quite useful.
When you need to work out the exact measurement of the surface inside one of these four-sided figures, there's a particular method that always delivers the right answer. It involves looking at a couple of key measurements of the shape itself. You don't need to be a math whiz to grasp this concept; it’s more about understanding which bits of information you need and where to put them. That, is that, it’s really about applying a simple recipe to get your result.
This approach to finding the area of a trapezoid is a fundamental idea in working with shapes, and it helps us make sense of how much room things take up. Whether you're trying to figure out how much paint you'd need for a wall shaped like this, or maybe just trying to solve a problem in a book, having this tool in your mental toolkit is a big help. It's a way to quantify the surface coverage, you know, just a little bit of geometry that makes a lot of sense.
Table of Contents
- What Exactly is a Trapezoid, Anyway?
- Getting to Know the Parts of the Trapezoid Area Formula
- How Do We Actually Figure Out the Trapezoid Area Formula?
- Breaking Down the Trapezoid Area Formula - Step by Step
- Why Does the Trapezoid Area Formula Work That Way?
- Real-World Scenarios for the Trapezoid Area Formula
- Is There Just One Trapezoid Area Formula to Remember?
- Keeping the Trapezoid Area Formula Handy
What Exactly is a Trapezoid, Anyway?
Before we jump into the numbers, it’s helpful to get a good picture of what a trapezoid actually looks like. Think of it as a four-sided shape, but with a special characteristic: two of its sides are always running parallel to each other. These two parallel sides are what we call the "bases" of the trapezoid. The other two sides are not parallel, and they can be sloped. So, it's almost like a rectangle that's been tilted or had one of its top corners pushed over a bit. It’s a pretty common shape, actually, appearing in all sorts of places, you know, like the top of a picnic table or the cross-section of a ditch.
The amount of room inside this shape, the surface it covers, is what we mean by its area. Imagine you're painting a flat piece of wood cut into this particular form; the area would tell you how much paint you'd need to cover it completely. It’s the total extent of the flat surface. That's what we are trying to figure out with the trapezoid area formula. It’s a measurement of two dimensions, basically, how wide it is and how tall it is, in a way that accounts for its unique shape. Very important for practical applications, too.
Unlike a simple square or a rectangle where all angles are right angles, a trapezoid can have a bit more variety in its corners. But the key feature, those two parallel sides, is what makes it a trapezoid and what allows us to use a specific, quite clever, formula to find its area. It’s a bit different from a general four-sided figure, which might be called a quadrilateral, because of that one specific parallel pair. So, that's what makes it special, and that's why it gets its own particular area calculation method.
Getting to Know the Parts of the Trapezoid Area Formula
To really get a handle on the trapezoid area formula, we need to meet its main characters. There are three key measurements we always look for when working with this shape. First, we have the two parallel sides, which we call the "bases." Let's just call them 'a' and 'b' for simplicity, or sometimes 'base 1' and 'base 2'. It doesn't really matter which one you call 'a' and which one you call 'b' because, you know, they're going to be added together anyway. So, it's pretty flexible in that regard. These are the lengths of the flat top and bottom edges, or the two sides that never meet.
Then, there's the third important measurement: the height. This isn't the length of one of the slanted sides, mind you. The height, often represented by 'h', is the straight-up-and-down distance between those two parallel bases. Imagine dropping a perfectly straight line from one base to the other, making a right angle with both. That's your height. It's a bit like measuring how tall a person is, but for the shape itself, from its lowest parallel edge to its highest. That’s what 'h' stands for in the trapezoid area formula, very important for the calculation.
So, to recap, you've got two bases (the parallel bits) and one height (the straight distance between them). These three pieces of information are all you need to figure out the amount of room inside any trapezoid. The trapezoid area formula basically tells you how to combine these three numbers in a specific way to get the final area measurement. It's like having all the ingredients for a recipe, and the formula tells you exactly how to mix them. Pretty neat, if you ask me, and it usually works out quite nicely.
How Do We Actually Figure Out the Trapezoid Area Formula?
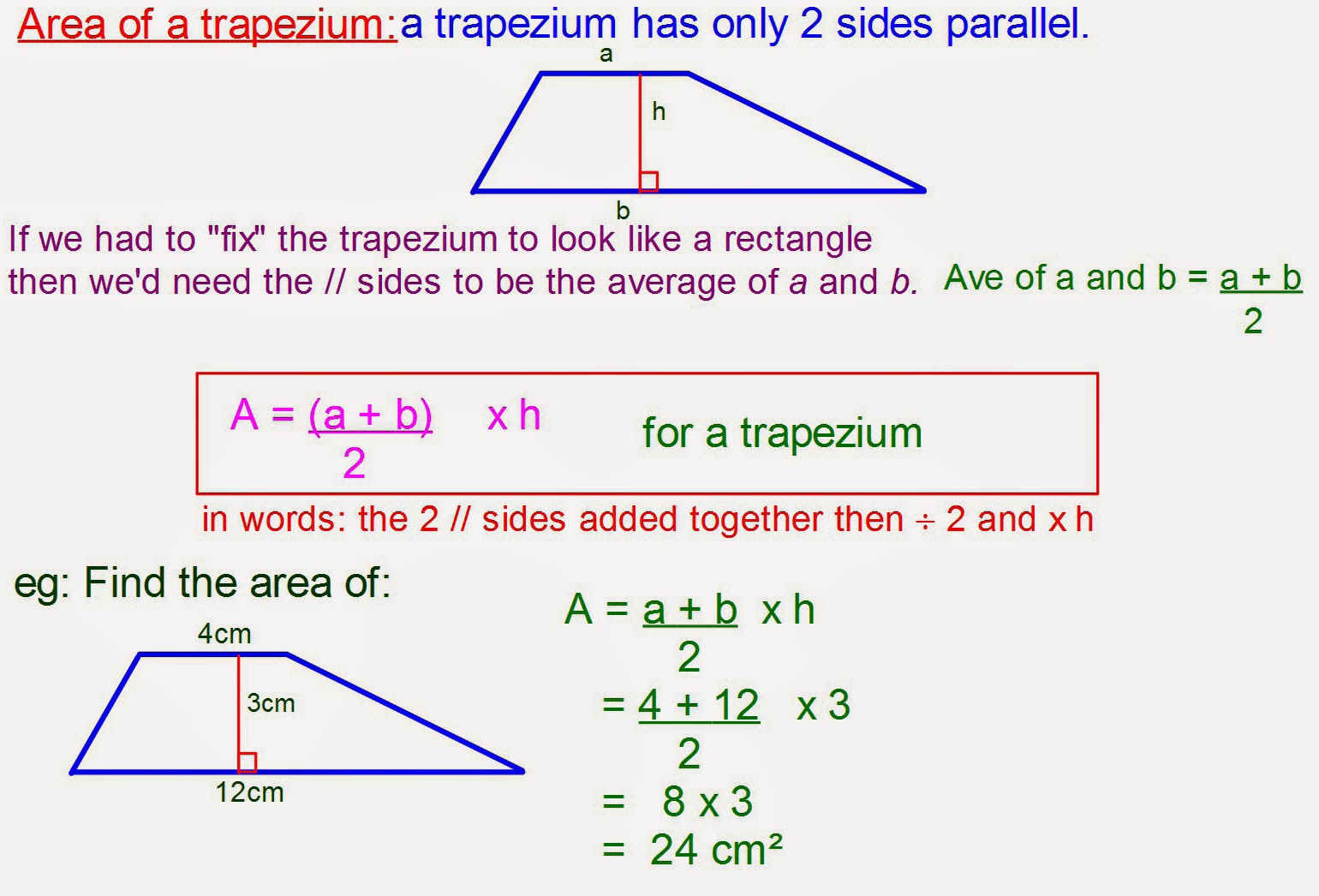
Alright, so you've got your trapezoid, and you've measured its two parallel bases and its straight-up height. Now comes the fun part: putting those numbers to work. The most common way to figure out the area of a trapezoid involves a specific little equation. It looks like this: Area equals one-half times the sum of the two bases, all multiplied by the height. Or, to put it with letters, A = ½ (a + b)h. This is the main trapezoid area formula that most people learn and use. It’s a pretty simple setup, honestly, just a few basic arithmetic operations.
Let's break down that trapezoid area formula just a little bit more. The first thing you do is add the lengths of your two bases together. So, if one base is 4 units long and the other is 6 units long, you'd add 4 and 6 to get 10. That sum represents a kind of "average width" for the trapezoid, which is a pretty clever way to think about it. Then, you take that sum and multiply it by the height of the trapezoid. So, if your height was 5 units, you'd multiply 10 by 5 to get 50. And finally, you take half of that result. So, half of 50 would be 25. That's your area! It’s a straightforward sequence of actions, you know, just a few steps.
This formula works for any trapezoid, no matter how wide or narrow, or how tall or short it might be. As a matter of fact, it's a very reliable way to get the correct area every single time, as long as your initial measurements are accurate. The idea of taking half of the product of the sum of the bases and the height is what makes this trapezoid area formula so effective. It’s a bit like finding the area of a rectangle that has the same height but an "average" base length. That’s why it’s so versatile, you know, for all sorts of shapes.
Breaking Down the Trapezoid Area Formula - Step by Step
Let's walk through the process of using the trapezoid area formula with a bit more detail, just to make sure it's super clear. First off, your primary job is to identify and measure the length of each base. These are the two sides that are parallel to each other. Let's say one of them is 7 units long, and the other is 11 units long. You'll want to write those numbers down. It’s like gathering your ingredients before you start cooking, you know, getting everything ready. Very important to get these right.
Next, you need to find the height of the trapezoid. Remember, this is the straight-up-and-down distance between those two parallel bases, not the slanted sides. So, if you measure that distance and it comes out to be, say, 6 units, then that's your 'h'. Once you have these three numbers – the two base lengths and the height – you're ready to plug them into the trapezoid area formula. It's really that simple, you know, just finding those specific measurements. This is where the magic happens, actually.
Now, for the actual calculation part. You'll take your first base (7) and add it to your second base (11). That gives you 18. Then, you take that sum (18) and multiply it by the height (6). So, 18 times 6 equals 108. Finally, you take half of that result. Half of 108 is 54. And there you have it – the area of your trapezoid is 54 square units. That's the whole process, really, using the trapezoid area formula to get your answer. It’s a pretty neat way to calculate the space, you know, quite efficient.
Why Does the Trapezoid Area Formula Work That Way?
It's natural to wonder why the trapezoid area formula is structured the way it is. Why do we add the bases, multiply by the height, and then divide by two? Well, think about it this way: a trapezoid can kind of be thought of as a rectangle that's had its top or bottom stretched or shrunk a bit. If you were to take two identical trapezoids and flip one upside down, then put them together, they would form a parallelogram. And the area of a parallelogram is simply its base times its height. So, you know, it’s a clever way to visualize it.
When you combine those two identical trapezoids to make a parallelogram, the base of that new parallelogram would be the sum of the two bases of your original trapezoid (a + b). And the height of the parallelogram would be the same as the height of your trapezoid (h). So, the area of that combined parallelogram would be (a + b) times h. But since that parallelogram is made up of *two* of your original trapezoids, to find the area of just *one* trapezoid, you simply take half of the parallelogram's area. That's where the "½" comes from in the trapezoid area formula. It’s actually pretty smart, if you think about it, a really elegant solution.
Another way to look at it is that the trapezoid area formula essentially finds the "average" length of the two parallel bases and then multiplies that average by the height. If you add the two bases and divide by two, you're getting their average length. Then, multiplying that average length by the height gives you the area, just like you would for a rectangle with that average length as its base. So, in essence, the formula for the area of a trapezoid is basically the average width times the straight-up distance. It's a conceptually simple idea, really, when you break it down, you know, quite intuitive.
Real-World Scenarios for the Trapezoid Area Formula
Knowing how to work with the trapezoid area formula isn't just for school assignments; it comes in handy in a bunch of different real-life situations. For instance, if you're helping someone design a garden bed that has a trapezoidal shape, you'd need to figure out its area to know how much soil or mulch to buy. Or, if you're a carpenter building a deck and one section needs to be shaped like a trapezoid, you'd use this formula to make sure you cut the right amount of wood. It's quite practical, honestly, for planning and building things.
Think about construction or architecture, too. Many parts of buildings, like certain roof sections, windows, or even the footprint of a uniquely shaped room, might be trapezoidal. To calculate the materials needed – glass for a window, tiles for a floor, or the surface area for painting – the trapezoid area formula becomes a very important tool. It helps professionals in these fields get their measurements accurate, which saves time and money. It’s a truly useful bit of math, you know, for making things happen in the real world.
Even in less obvious places, like certain parts of engineering designs or when calculating the flow of water in a channel that has a trapezoidal cross-section, this formula is applied. It helps people understand the capacity or the surface coverage of various components. So, while it might seem like a simple geometry concept, its applications stretch across many different fields. It’s a fundamental calculation that helps us understand and interact with the physical spaces around us, you know, quite broadly applicable.
Is There Just One Trapezoid Area Formula to Remember?
When you're looking for the trapezoid area formula, you might come across a few slightly different ways it's written, but they all basically mean the same thing. The most common one, as we've talked about, is A = ½ (a + b)h. Sometimes, you might see it written as A = (a + b) × h / 2, which is just doing the division by two at the end instead of multiplying by one-half at the beginning. It's really the same mathematical operation, just presented a little differently. So, you know, don't get too worried if you see a slight variation.
Another common way to write the trapezoid area formula is using 'base 1' and 'base 2' instead of 'a' and 'b'. So, it might appear as: Area of trapezoid = ½ × h × (base 1 + base 2). This is just a different naming convention for the bases, but the process of adding them together, multiplying by the height, and then taking half remains exactly the same. It's like calling a friend by their first name or their nickname; it's still the same person, just a different way of referring to them. It's pretty consistent, actually, no matter how it’s written.
So, to answer the question directly, while the exact presentation of the trapezoid area formula might vary a little bit, the core idea and the mathematical operations involved are always consistent. You're always going to be adding the lengths of the two parallel sides, multiplying that sum by the straight-up distance between them, and then dividing the whole thing by two. As a matter of fact, it's a very dependable calculation that works every time. So, just pick the version that makes the most sense to you and stick with it; they all lead to the same correct answer.
Keeping the Trapezoid Area Formula Handy
Having a solid grasp of the trapezoid area formula is a really helpful skill, whether you're a student, a DIY enthusiast, or someone who just likes to understand how things work. It's a simple yet powerful tool for measuring the surface amount of a specific kind of four-sided shape. Remember, the key pieces of information you need are the lengths of the two parallel bases and the straight-up height between them. Once you have those, the formula A = ½ (a + b)h will guide you to the correct answer every single time. It's a pretty straightforward calculation, you know, once you get the numbers.
The amount of room inside a trapezoid, that grey space you might see in a diagram, is what this formula helps you uncover. It’s the surface coverage within its outer edges. This particular formula is a specific method that works for any trapezoid, regardless of its specific slant or overall dimensions, as long as it has those two parallel sides. So, keep this formula in your mind, or maybe even jot it down somewhere you can easily find it. It's a bit like having a secret code for understanding shapes, you know, quite useful.
Understanding this basic geometry concept opens up a lot of possibilities for working with shapes in practical ways. From figuring out how much material you need for a project to solving problems that involve oddly shaped spaces, the trapezoid area formula is a fundamental piece of knowledge. It’s a calculation that has wide-ranging applications, so it's a good one to have ready. And that's pretty much it, really, for understanding how to measure the space inside a trapezoid. It's a skill that definitely comes in handy, you know, more often than you might think.

Lesson Video: Area of a Trapezoid | Nagwa

Area of a Trapezoid: Formula and 5 Examples | Livius Prep
Trapezoid Area